前言

流程

回歸問題預測連續(xù)值,在某個區(qū)間內(nèi)變動.
常見的線性回歸問題模型是y=ax+b,然而現(xiàn)實世界由于大量的數(shù)據(jù)偏差以及復雜度,同時還有大量的噪聲,往往達不到如此的精確解,實際解決問題時需要考慮噪聲的存在

對于噪聲,往往我們已經(jīng)假設(shè)了它符合高斯0-1分布,如果噪聲是隨機的就無法推算了

問題在于這組數(shù)據(jù)是如何分布的

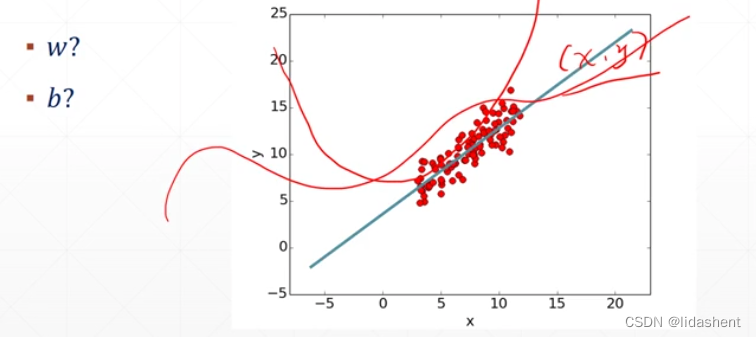
一小組數(shù)據(jù)在某個區(qū)間內(nèi)的函數(shù)圖像究竟是如何?
如何去求解wb?來自主優(yōu)化其數(shù)據(jù)迭代?
在此之前設(shè)定一個評價函數(shù)

預測值和真實值得平方和越來越小時,loss函數(shù)將起作用
問題是如何自動更新合適的w和b來達到這個效果?
要確保w和b快速收斂,準確的沿數(shù)據(jù)的變化走向進行預測,loss越小越準
準確的說w和b沿著loss函數(shù)下降的方向前進

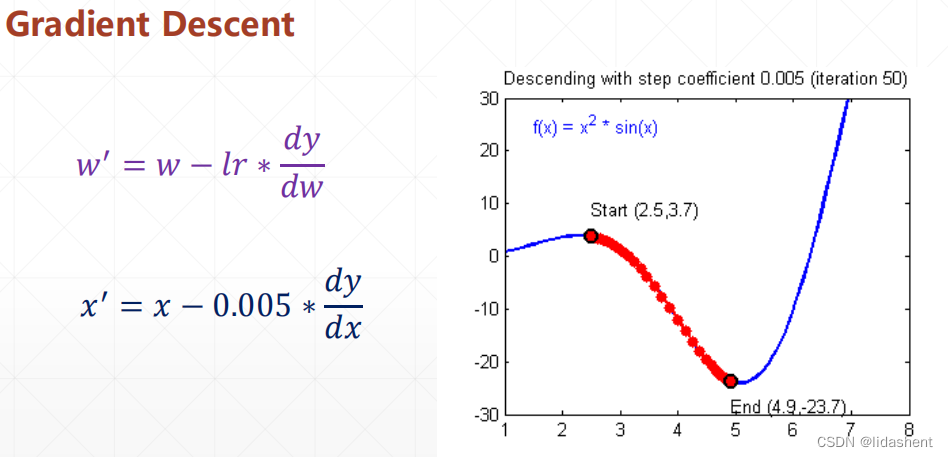
lr代表步長,這個需要合適設(shè)置避免進入相對最小值
衰減因子則代表著沿著增大的導數(shù)的反方向前進,如果導數(shù)為正,則是圖像是數(shù)據(jù)增大方向,則x變小尋找山谷,如果導數(shù)為負,則圖像數(shù)據(jù)減小方向,則x增大,尋找山谷如是
(數(shù)據(jù)圖像,導數(shù)圖像,對導數(shù)的變化求最小值的方向)
比如當前位置3.2,導數(shù)-23.3 則,位移變化方向是 3.3165
x=3.2-(-23.3*0.005) x2=x-△w
這只是w的一種情況,然后看b,二維向量圖,從隨機點開始進行梯度下降

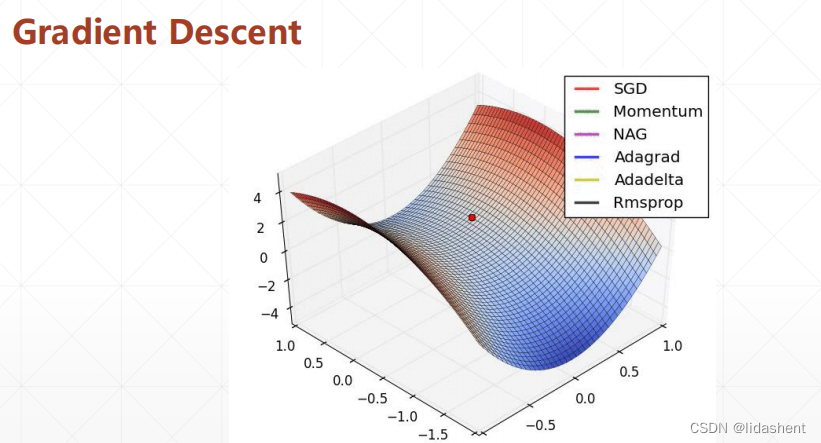
三個軸分別代表了w,b和z軸loss,
公式為

運行后會自動找到合適的wb對數(shù)據(jù)進行公式建模
預測值和真實值之間的平方差成為了loss函數(shù)，這樣將求解最佳wb的問題變成了求解最小loss的問題
然后loss代表梯度，w和b向著梯度減小的方向前進，每次梯度變化可能非常大，因此需要進行步伐控制
δloss代表平均值loss.總loss/len樣本數(shù)量
因此計算loss代碼為

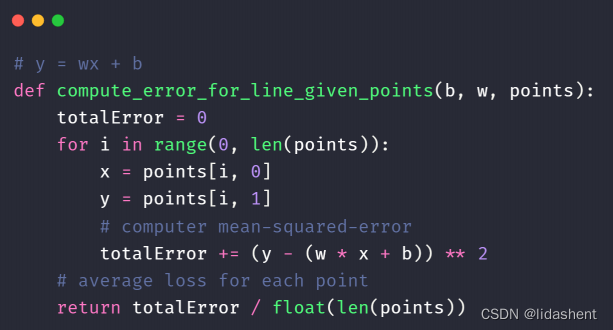
數(shù)學原理

x^2求導得到2x,所以δloss/δw=2xxxxx +2xxxxx…
b導數(shù)為1,因此…
根據(jù)loss對w和b的導數(shù),確定那里是梯度下降的方向,對w和b進行更新,變相的求loss下降的方向
代碼實現(xiàn)為:

然后不斷迭代就得到了應(yīng)有的w和b權(quán)重

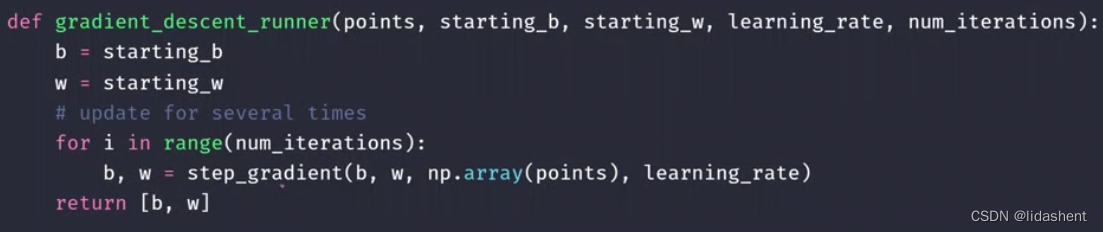
基于線性模型建立的有如下三種
線性模型
二分類模型(sigmod函數(shù)用于劃分01)
多分類模型

案例操作

使用numpy實現(xiàn)與tensorflow對比實現(xiàn)兩者
tensorflow2.4運行即可,帶數(shù)據(jù)與代碼
https://www.aliyundrive.com/s/LmAms9tzWdq