線(xiàn)性可分SVM中，若想找到分類(lèi)的超平面，數(shù)據(jù)必須是線(xiàn)性可分的；但在實(shí)際情況中，線(xiàn)性數(shù)據(jù)集存在少量的異常點(diǎn)，導(dǎo)致SVM無(wú)法對(duì)數(shù)據(jù)集線(xiàn)性劃分

也就是說(shuō)：正常數(shù)據(jù)本身是線(xiàn)性可分的，但是由于存在異常點(diǎn)數(shù)據(jù)，導(dǎo)致數(shù)據(jù)集不能夠線(xiàn)性可分

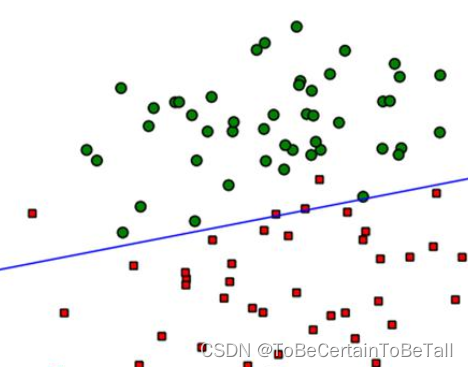
一. 軟間隔模型

為了解決上述問(wèn)題，我們引入軟間隔的概念：

1. 松弛因子的解釋

• 硬間隔： 線(xiàn)性劃分SVM中的硬間隔是距離度量；在線(xiàn)性劃分SVM中，要求函數(shù)距離一定是大于等于1的，最大化硬間隔條件為：$$\{\begin{array}{c}min\frac{1}{2}{\Vert \overrightarrow{w}\Vert }^2\\ s.t：y^{(i)}({\omega }^T?x^{(i)}+b)\ge 1，i=1,2,...,m\end{array}$$
• 軟間隔：SVM對(duì)于訓(xùn)練集中的每個(gè)樣本都引入一個(gè)松弛因子(ξ)，使得函數(shù)距離加上松弛因子后的值是大于等于1；$$y^{(i)}({\omega }^T?x^{(i)}+b)\ge 1?\xi ；i=1,2,...,m，\xi \ge 0$$

松弛因子(ξ)表示：相對(duì)于硬間隔，對(duì)樣本到超平面距離的要求放松了

當(dāng) $\xi =0$ ， 相當(dāng)于硬間隔
當(dāng) $0<\xi <1$ ， 相當(dāng)于樣本點(diǎn)位于“街”內(nèi)
當(dāng) $\xi >1$ ， 相當(dāng)于樣本點(diǎn)位于“街”對(duì)面
當(dāng) $\xi >2$ ， 相當(dāng)于樣本點(diǎn)位于“街”對(duì)面外側(cè)

注意：$\xi$只能對(duì)少量的樣本起作用

$\xi$越大，表示樣本點(diǎn)離超平面越近，
$\xi >1$，那么表示允許該樣本點(diǎn)分錯(cuò)

因此：加入松弛因子是有成本的，過(guò)大的松弛因子可能會(huì)導(dǎo)致模型分類(lèi)錯(cuò)誤

所以，我們對(duì)存有異常點(diǎn)的數(shù)據(jù)集劃分時(shí)，目標(biāo)函數(shù)就變成了：
$$?\begin{array}{c}min\frac{1}{2}{\Vert \overrightarrow{w}\Vert }^2+C{\sum }_{i=1}^n{\xi }_{(i)}\\ \\ y^{(i)}({\omega }^T?x^{(i)}+b)\ge 1?{\xi }^{(i)}，i=1,2,...,m\end{array}$$
$$\xi i\ge 0，i=1,2,...,m$$

公式$C{\sum }_{i=1}^n{\xi }_{(i)}$表式：
?
????每個(gè)樣本懲罰項(xiàng)的總和不能大，函數(shù)中的C>0是懲罰參數(shù)，需要調(diào)參

C越大，表示對(duì)錯(cuò)誤分類(lèi)的懲罰越大，也就越不允許存在分錯(cuò)的樣本；
?
C越小表示對(duì)誤分類(lèi)的懲罰越小，也就是表示允許更多的分錯(cuò)樣本存在

也就是說(shuō)：
對(duì)于完全線(xiàn)性可分的數(shù)據(jù)來(lái)說(shuō)，C的值可以給大一點(diǎn)
對(duì)于線(xiàn)性可分但存在異常的數(shù)據(jù)來(lái)說(shuō)，C的值需要調(diào)小

小節(jié)

對(duì)于線(xiàn)性可分的m個(gè)樣本(x1,y1)，(x2,y2)… ：

	x為n維的特征向量y為二元輸出，即+1，-1

SVM的輸出為w，b，分類(lèi)決策函數(shù)

選擇一個(gè)懲罰系數(shù)C>0，構(gòu)造約束優(yōu)化問(wèn)題

$$\{\begin{array}{c}{\min }_{\beta \ge 0}\frac{1}{2}{\sum }_{i=1}^m{\sum }_{j=1}^m{\beta }_i{\beta }_j{y}^{(i)}{y}^{(j)}{x}^{(j{)}^T}{x}^{(i)}?{\sum }_{i=1}^m{\beta }_i\\ s.t:{\sum }_{i=1}^m{\beta }_i{y}^{(i)}=0，0\le {\beta }_i\le C，i=1,2,...,m\end{array}$$
使用SMO算法求出上述最優(yōu)解$\beta$
找到所有支持向量集合：
$$S=(x^{(i)},y^{(i)})(0<{\beta }_i<C,i=1,2,...,m)$$
從而更新w，b

$w={\sum }_{i=1}^m{\beta }_i{x}^{(i)}{y}^{(i)}$

$b=\frac{1}{S}{\sum }_{i=1}^S(y^s?{\sum }_{i=1}^m{\beta }_i{x}^{(i{)}^T}{y}^{(i)}{x}^s)$

構(gòu)造最終的分類(lèi)器，為：
$$f(x)=sign(w?x+b)$$

	x<0時(shí)，y=-1x=0時(shí)，y=0x>0時(shí)，y=1注意：假設(shè)，不會(huì)出現(xiàn)0若出現(xiàn)，正負(fù)樣本隨意輸出一個(gè)，即+0.00000001或-0.00000001都可以

2. SVM軟間隔模型總結(jié)

	可以解決線(xiàn)性數(shù)據(jù)中存在異常點(diǎn)的分類(lèi)模型構(gòu)建問(wèn)題通過(guò)引入松弛因子，可以增加模型的泛化能力，即魯棒性；對(duì)于模型而言：如果給定的懲罰項(xiàng)系數(shù)C越小，表示在模型構(gòu)建的時(shí)候，就允許存在越多的分類(lèi)錯(cuò)誤的樣本，也就表示此時(shí)模型的準(zhǔn)確率會(huì)比較低；如果懲罰項(xiàng)系數(shù)越大，表示在模型構(gòu)建的時(shí)候，就越不允許存在分類(lèi)錯(cuò)誤的樣本，也就表示此時(shí)模型的準(zhǔn)確率會(huì)比較高。

---

感謝閱讀🌼
如果喜歡這篇文章，記得點(diǎn)贊👍和轉(zhuǎn)發(fā)🔄哦！
有任何想法或問(wèn)題，歡迎留言交流💬，我們下次見(jiàn)！

祝愉快🌟！

---